Activité 1 : Découverte des accéléromètres

Previous Next



Le smartphone a réellement changé notre quotidien : Jeux, réseaux sociaux, musiques, photos, vidéos, GPS...: Il y avait 4 milliards de téléphones sur la planète en 2009, il y en a aujourd'hui 7,8 milliards. Il y a environ 54 téléphones vendus par seconde.


Sans réfléchir nous pivotons sans cesse notre smartphone pour accéder à de nouvelles fonctions ou pour voir des photos et vidéos en plein écran


Regardez attentivement la vidéo suivante en cliquant sur l'image




Nous allons donc nous pencher sur la problématique suivante :


Comment un smartphone connaît-il son orientation dans l'espace ?


La première étape va consister à déterminer le positionnement des axes X, Y et Z comme dans la vidéo à 1min16s

Fig.1 : Représentation simplifiée accéléromètre 3 axes


Fig. 2 :Axes accéléromètre smartphone


Comme expliqué dans la vidéo, lorsqu'un axe de l'accéléromètre est positionné verticalement, il mesure l'accélération de la pesanteur g=9,81 m.s-2 : représenté par le vecteur bleu ci-dessus

  1. Sur votre smartphone allez sur le PlayStore et telechargez l 'appli accelerometer meter et installez-la

Sélectionnez Meter

Positionnez votre smartphone verticalement, horizontalement puis à plat sur la table


A partir des informations de l'appli déterminez le nom  de l'axe vertical (X;-X ;Y;-Y et Z;-Z)


Copiez Fig.2 sur votre compte rendu et remplacer les ? par X, Y ou Z


Remarque : Les couleurs de X, Y et Z n'ont pas de liens avec les couleurs des sphères de la Fig.1


Nous allons maintenant réaliser une appli Android qui va afficher les valeurs des accélérations sur les axes X, Y et Z

Cette appli sera développée sur le logiciel en ligne Appinventor2 (AI2) et sera ensuite exécutée sur votre smartphone


  1. Prenez connaissance de l'environnement d'AI2 en visionnant la vidéo ci-dessous en cliquant sur l'image




  1. Consultez la fiche méthode de travail dans Ressources

Installez sur votre smartphone l'appli MIT AI2 Companion à partir du PlayStore

Sur votre PC ouvrez un navigateur internet  (Firefox ou chrome ) puis tapez "Appinventor 2" puis                rendez vous sur le site.

Créez un nouveau projet sur AI2 que vous nommerez Inclinomètre suivi des deux noms des deux                personnes de l'équipe et de la classe. Exemple : Inclinomètre_Michel_Durand_206 sans accent et un "_"        entre noms et classes (pas d'espace vide !!!)


       Suivez pas à pas le tuto ci-dessous et effectuez les mêmes opérations sur votre ordinateur


Nommez votre appli comme suit:



  1. Installez votre appli sur votre smartphone en utilisant le QR code


- Si au moment de l'installation vous avez un message de ce type :


Choisissez l'option  : INSTALLER QUAND MEME


       - Si après avoir scanné le QR code rien ne se passe ou l'appli ne s'installe pas, copier l'adresse proposée        sur votre smartphone


Exemple :



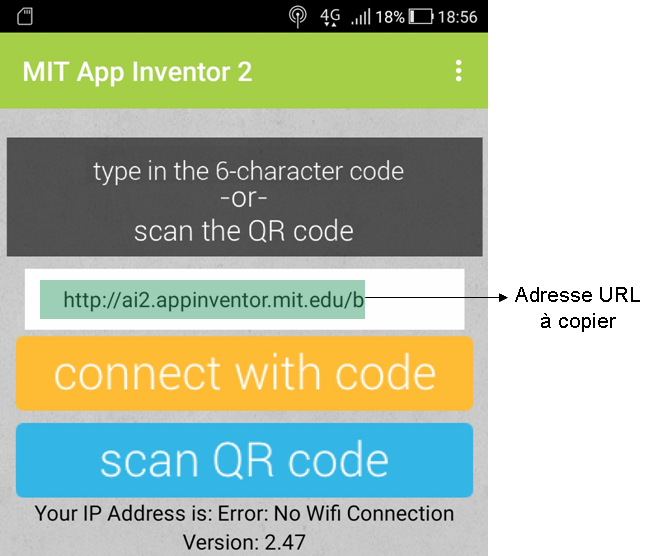
- Fermer toutes les fenêtres de votre navigateur internet et coller l'adresse URL dans votre barre de                recherche et valider


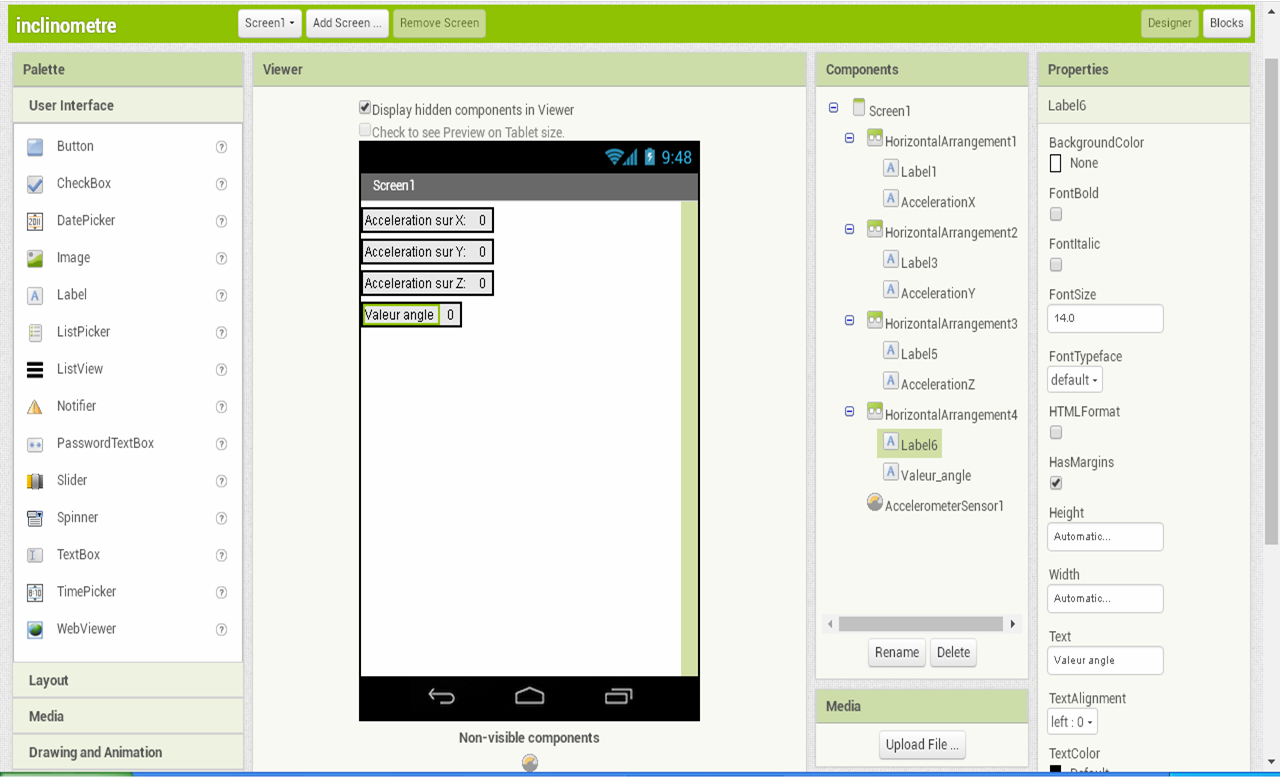
  1. Exécutez votre appli et vérifiez si les accélérations affichées sont cohérentes avec la réalité


On souhaite maintenant compléter votre programme (voir ci-contre) pour que votre smartphone affiche la valeur de l'angle qu'il a par rapport à la verticale .

Cette application se nomme inclinometre : C 'est une appli qui mesure des angles.

Pour cela il faut faire appel à des notions de trigonométrie vue en troisième


  1. Regardez la vidéo ci-dessous en cliquant sur l'image




  1. Dans la vidéo précédente la valeur de l'angle est de 33,7° . Quelle opération faut-il faire sur votre calculatrice pour trouver cette valeur ?


  1. Dans la partie Designer de AI2 rajouter un label Valeur angle comme vous l'avez déjà fait pour le label Accélération sur X de la question 3. Vous devez obtenir ceci :




Quel lien y a t-il entre le triangle de la question 6 et l'angle que nous devons afficher sur le smartphone ?


Regardez attentivement le schéma suivant qui montre l'évolution de l angle d'inclinaison  du smartphone (appelé ) ainsi que les projections sur les axes rouge et vert du vecteur


Nous voyons bien sur le schéma que  la valeur de l'angle varie quand on incline le smartphone.


Nous retrouvons d'une certaine manière le triangle ABC de la vidéo de la question 6.


La différence est que les valeurs des segments AB et BC ne sont pas en centimètres mais sont des accélérations en m.s-2 .Ces valeurs varient quand vous inclinez le smartphone


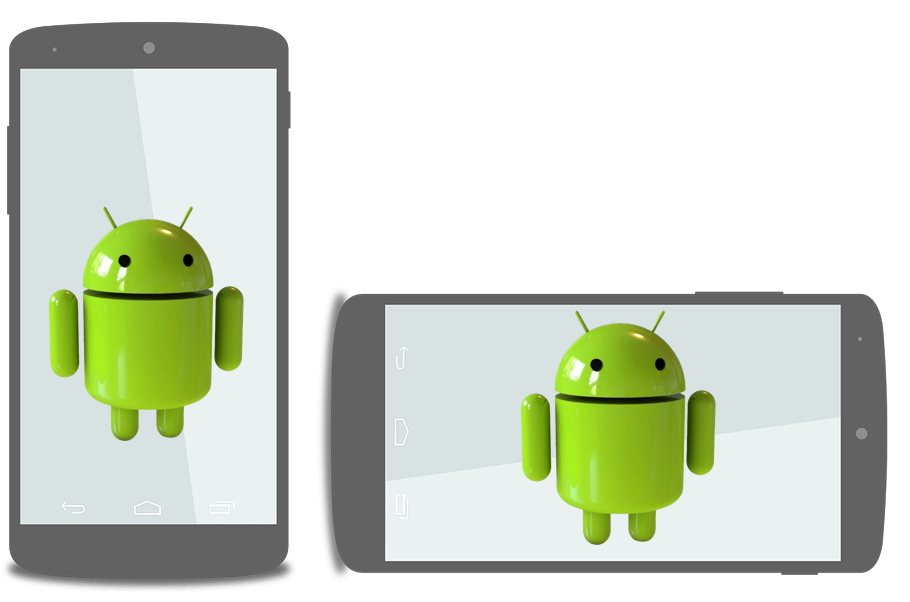
  1. A partir du triangle ABC et de la réponse à la question 7, écrire la relation entre , Accélération sur axe rouge et Accélération sur axe vert


  1. Complétez alors votre programme pour qu'il puisse calculer les valeurs de l'angle pour cela utilisez le menu Math




Tous les smartphones sont équipés de la fonction rotation automatique : Elle permet d'afficher des images ou des vidéos que votre smartphone soit en position "verticale" ou "horizontale"

Vous allez désactiver cette fonction sur votre smartphone et vous allez modifier votre programme pour qu'il affiche une image quelque soit son orientation comme ci-dessous :




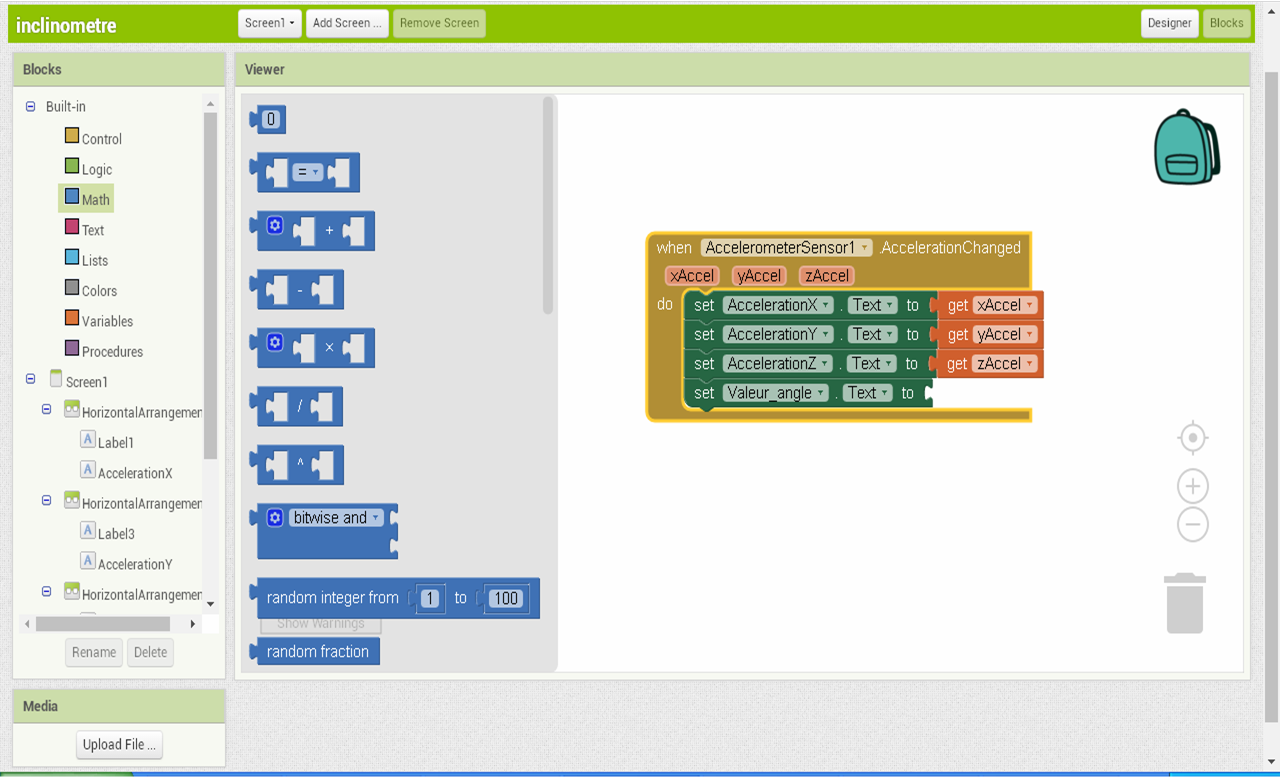
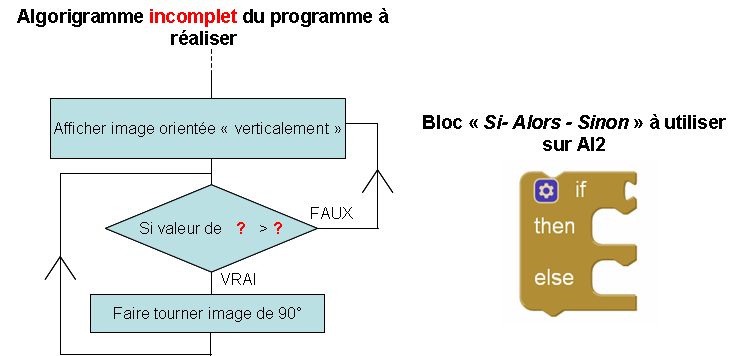
L' image ci-dessous représente l' algorigramme de la partie du programme que vous devez réaliser et le bloc sur AI2 que vous devez utiliser





  1. Chercher sur Internet la définition d'un algorigramme


  1. Déterminer ce qu'il faut mettre à la place des ? pour que l'image tourne quand le smartphone est à l'horizontale


  1. Pour réaliser le programme sur AI2, vous allez tout d'abord télécharger l'image à afficher en cliquant ICI

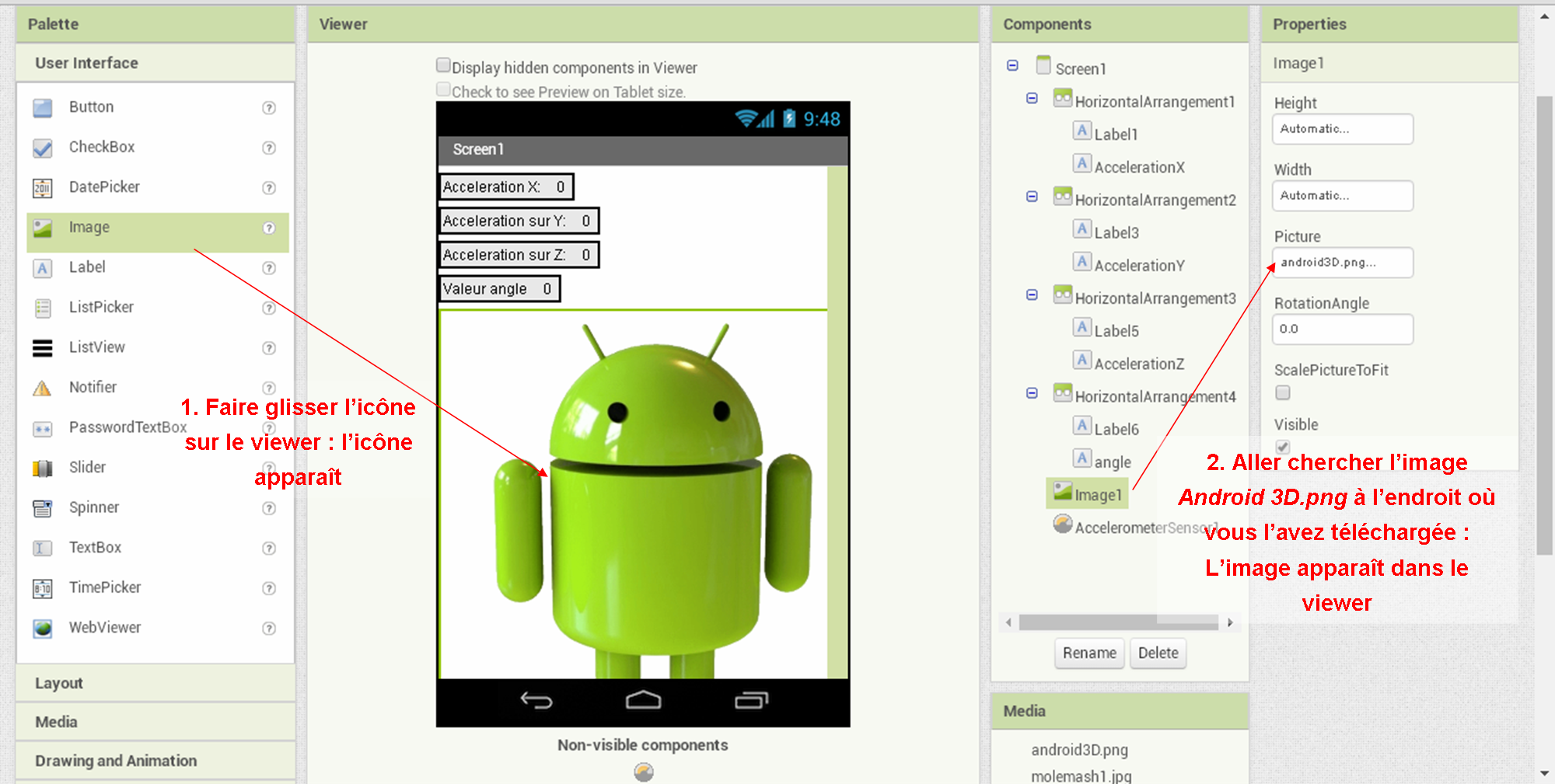
       Enregistrez-la dans votre espace de travail : Mes Documents/SNT/objets connectés


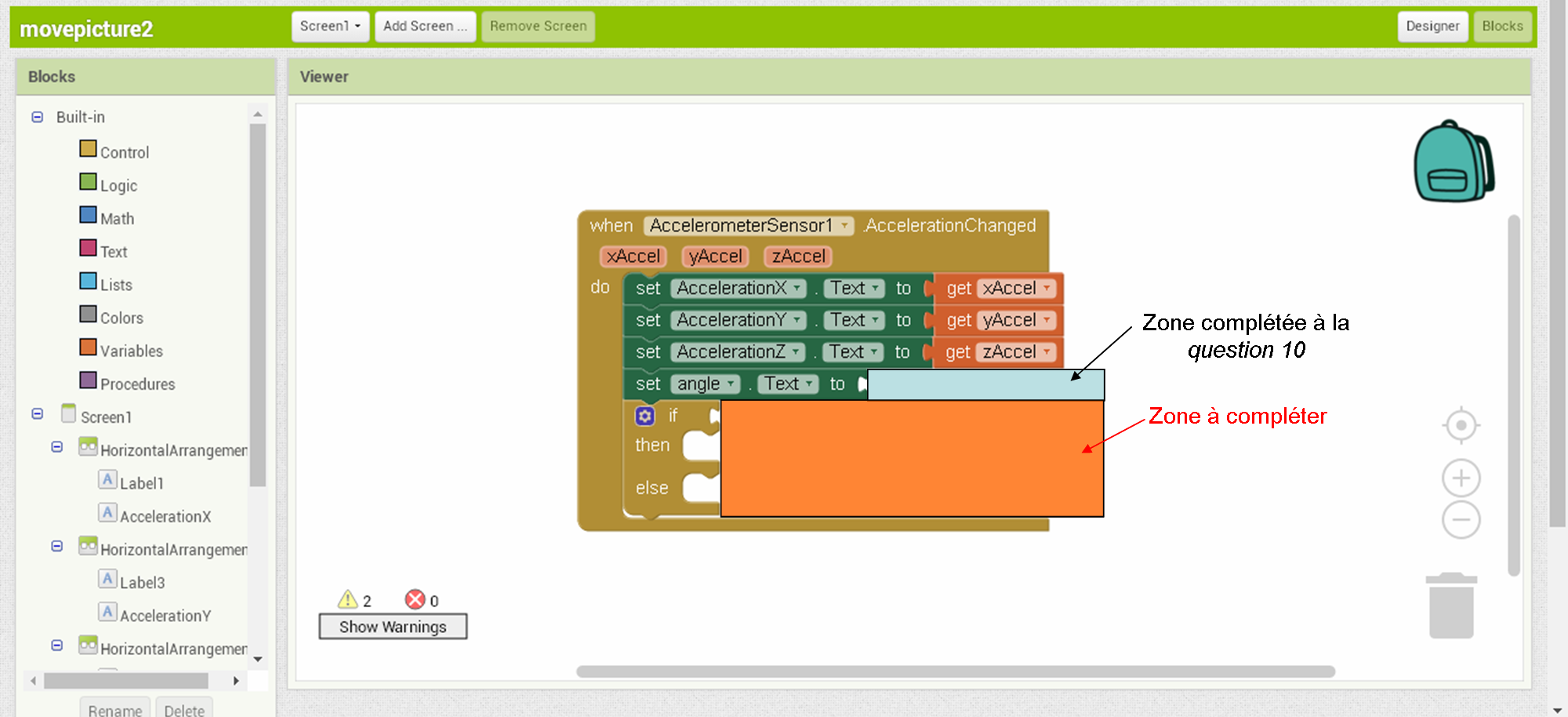
  1. Insérer l'image Android 3D en suivant ce mode opératoire:




  1. Insérez le bloc "Si-Alors-Sinon" comme sur l'image ci-dessous


Votre programme va se présenter sous cette forme




  1. Compléter votre programme, sauvegardez-le et télécharger-le sur votre smartphone


  1. Testez le fonctionnement et modifier le programme si nécessaire en cas de dysfonctionnement






Créé avec HelpNDoc Personal Edition: Générateur d'aides Web gratuit